一、直线设计

直线是平面线形设计的基本要素之一，具有距离短、易布设等特点，在公路中使用最为广泛。两点之间以直线为最短，给人以短捷、直达的良好印象，加之汽车在直线上行驶受力简单，方向明确，驾驶操作简易。但直线线形缺乏灵活性，大多难于与地形、地物相协调；强定直线，往往造成工程量大，破坏自然条件。过长的直线易使驾驶人员感到单调、疲倦，难以目测车间距离，易于产生尽快驶出直线的急路躁情绪。长直线还容易导致致高速行驶，危及交通安全。

下述路段可适宜采用直线：

（1）不受地形、地物限制的平坦地区或山间的开阔谷地；

（2）市镇及其近郊，或规划方正的农耕区等以直线条为的地区；

（3）长大桥梁、隧道等式逻辑构造物物路段；

（4）路线交叉点其前后；

（5）双车道公路提供超车的路段。

在设计中，过长和过短的直线都不是好的线形。因此对直线的最大和最小长度都要加以限制。

1、直线的最大长度

关于直线的极限长度（最大与最小长度），从理论上求解是非常困难的，主要应根据驾驶人员的视觉效果和心理上的承受能力来确定，目前尚在研究中。各国都从经验出发，通过调查确定限制最大直线长度。如德国规定不超过计算行车速度（Km/h）的20倍，原苏联规定为8km，美国为3mile（4.83km）。我国已建成的位于平原微丘区的十多条高速公路的直线长不超过3200m；沈大高速公路多处出现5km至8km的长直线，最大13km。据国内外调查研究结果，最大直线长度为以汽车按计算行车速行驶70s左右的距离控制为宜。

经过对不同路段，按100km/h的行驶车速对驾驶人员和乘客调查其心理反应和感受，有如下结果：

（1）位于城市附近的道路，作为城市干道的一部分，由于路旁高大建筑和多彩的城市风光，无论路基高低均被纳入视线范围，驾驶员和乘客无直线过长希望驶出的不良反应；

（2）位于乡间平原区的公路，随季节和地区不同，驾驶人员有不同反应。北方的冬季，绿色枯萎，景色单调，太长的直线使人情绪被纳入受到影响。夏天稍许改善一些，但驾驶人员加速行驶希望尽快驶完直线的心理普遍存在；

（3）位于大戈壁，大草原的公路，直线长度可达数十公里，司乘人员极度疲劳。车速超过设计速度很多。但在这种特殊的地形条件下，除了直线别无其它选择，人为设置弯道不但不能改善其单调，反而增加路线长度。

由此看来，直线的最大长度，在城镇附近或其它景色有变化的地点大于20v是可以接受的；在景色单调的地点最好控制在20v以内；而在特殊的地理条件下应特殊处理，若作某种限制看来是不现实的。直线 的最大长度应与地形相适应，与景观相协调，不强定长直线，也不硬性设置不必要的曲线。

当采用长的直线形时，为弥补景观单调之缺陷，应结合沿线具体情况采取相应的技术措施并注意下述问题：

（1）在长直线上纵坡不宜过大，因长直线再加下陡坡行驶更易导致高速度；

（2）长直线与大半径，凹形竖曲线组合为宜，这样可以使生硬呆板的直线得到一些缓和；

（3）道路两侧地形过于空旷时，宜采取植不同树或设置一定建筑雕广告牌等措施，以改善单调的景观。

（4）长直线或长下坡尽头的平曲线，除曲线半径、超高、视距等必须合规定外，还必须采取设置标志、增加路面抗滑能力等安全措施。

2、直线的最小长度

考虑到线形的连续和驾驶的方便，相邻两曲线之间应有一定的直线长度。

（1）同向曲线间的直线最小长度

互相通视的同向曲线间若插以短直线，容易产生把两个曲线看成是一个曲线的错觉，破坏了线形的连续性，易于造成驾驶操作的失误，设计中应尽量避免。由于这种线形组合所产生的缺陷是来自驾驶员的错觉，所以若将两曲线拉开，也就是限制中间直线的最短长度，使对向曲线在驾驶员的视觉以外则可以避免上述缺点。大量的观测资料证明，行车速度愈高，司机愈是注视远处的目标，这个距离在数值上大约是计算行车速度v(以km/h计)的6倍（以m计），所以同向曲线间的最短直线长度以不小于6v为宜。这种要求在车速较高的道路（v≥60km/h）上宜尽可能保证，而对于低速道路（v≤40km/h）的2倍为宜。在受到条件限制时， 宜将在同向曲线间插入大半径曲线或将两曲线作成复曲线、卵形曲线或C形曲线。

（2）反向曲线间的直线最小长度

两相反圆曲线之间，考虑到为设置超高和加宽缓和的需要以及驾驶人员转向操作的需要，其间的直线最小长度（以m计）以不小于计算行车速度（以km/h计）的2倍为宜。当直线两端高设有缓和曲线时，可直接相连构成S曲线，即两个反向圆曲线用缓和曲线直接相连。

三、四级公路上，两相邻反向曲线无超高、无加宽时，可径相衔接；无超高有加宽时，中间应没有长度不小于10m的加宽缓和段。工程特殊因难的山岭重丘区，三、四公路设置超高时，中间直线长度不得小于15m。

（3）相邻回头曲线间的直线最小长度

回头曲线是指山区公路为克服高差在同一坡面上回头展线时所采用的曲线。两回头曲线间，由一个回头曲线的终点到下一个回头曲线起点的距离，在二、三、四级公路上应分别不小于200m、150m和100m。

二、圆曲线

各级公路和城市道路不论转角大小均应设置平曲线，而圆曲线是平面线形中的主要组成部分。在平面线形中的单曲线、复曲线、虚交点曲线和回头曲线等，一般都包括有圆曲线：圆曲线由于与地形适应性强、可循性好、线形美观和易于测设等优点，使用十分普遍

1、计算公式及其影响因素

由第一章汽车行驶理论，根据汽车行驶在曲线上力的平衡式(1-1-31)可知圆曲线半径计算公式为

式中：v——各级公路的计算行车速度，km/h；

u——最大横向力系数；

i——路拱横向坡度，以小数计。

从上式可知，圆曲线半径越大．横向力系数就越小，汽车就越稳定。

所以从汽车行驶稳定性出发，圆曲线半径越大越好。但有时因受地形、地质、地物等因素的限制，圆曲线半径不可能设置得很大，往往会采用小半径的圆曲线，这时如果半径选用的太小，又会使汽车行驶不安全，甚至翻车。所以必须综合考虑汽车安全、迅速、舒适和经济，并兼顾美观，使确定的最小半径能满足某种程度的行车要求：这种最起码的半径数值，就是圆曲线的最小半径限制值。《公路工程技术标推》根据各级公路的不同要求，规定了圆曲线最小半径有三类：极限最小半径、一般最小半径和不设超高的最小半径。其中极限最小半径主要满足行车安全．适当考虑舒适性；—般最小半径已具有较好的安全性和舒适性；不设超高的最小半径是考虑即使不设超高也能保证其安全性和舒适性。

在一定车速v的条件下, 要满足三类最小半径不同要求的安全性和舒适性．关键在于横向力系数u值的合理确定。

(1)行车安全性分析

汽车在弯道上安全行驶的必要条件是轮胎不会在路面上产生滑移：即要求横向力系数u要小于或等于轮胎与路面间的横向摩阻力系数Ψ，即

式中；Ψ——轮胎与路面的横向摩阻系数，见表1-1-3。

(2)舒适性分析

根据国内外大量资料分析，乘客随u值的变化其心理反应如下：

当u〈0.1时，不感到有曲线存在，很平稳，近似于在直线上行驶；

当u＝0.15时，感到有曲线存在，但尚平稳；

当u＝0.2时，感到有曲线存在，略感不平稳；

当u＝0.35时，感到明显不平稳；

当u＝0.4时，感到非常不平稳．有倾倒的危险感。

由此可知，从乘客的舒适性出发，u值以不超过0.10为宜，最大不超过0.15~0.20。

(3)经济性分析

在确定u值时，还应考虑汽车运营的经济性。根据试验分析，汽车在弯道上行驶与直线相比，存在着以下关系：

横向力系数u 燃料消耗(％) 轮胎磨损(％)

0 100 100

0.10 110 220

0.15 115 300

0.20 120 390

综上分析，u值大小与行车安全、经济与舒适等密切相关。因此，u值的选用应根据行车速度、圆曲线半径及超高横坡度的大小，在合理的范围内选择。

2、圆曲线最小半径确定

(1)极限最小半径

极限最小半径是路线设计中各级公路所能允许的极限值，其u值的选用，主要满足安全要求，兼顾舒适性，因此在非特殊困难的情况下，一般不轻易采用。

极限最小半径可按下式计算

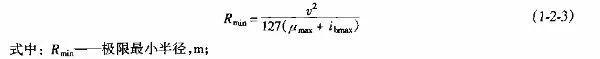
umax——极限最小半径所对应的横向力系数，见表1-2-1；

umin——最大超高横坡度，见表1-2-1。

极限最小半径横向力系数及超高横坡度取用表 表1-2-1

(2)一般最小平曲线半径

为避免在路线设计时只考虑节约投资，不考虑线形的整体协调和今后提高公路等级而过多采用极限最小半径的片面倾向，同时也要考虑在地形比较复杂的情况下不会过多地增加工程量，而且也具有充分的舒适感。为此，《公路工程技术标准》规定了“一般最小半径”。一般最小半径可按下式计算

式中：R一般———般最小半径，m；

ib——路拱超高横坡度，见表1-2-2；

u——一般最小半径所对应的横向力系数，见表1-2-2

一般最小圆曲线半径横向力系数及超高横坡度取用表

(3)不设超高的最小圆曲线半径

当路面不设超高时，路拱为双向横坡度，与直线段的路拱横坡度相同，当路线某一半径大于一定值时，即使汽车在圆曲线外侧行驶也能获得足够的安全性和很好的舒适性。不设超高的最小圆曲线半径可按下式计算

式中：R免——不设超高最小半径，m；

i1——路拱横坡度，二级及以上等级公路时，取i1＝0.01~0.02，二级以下公路时，取i1=0.03~0.04；

u——不设超高横向力系数，一般取u＝0.035~0.06。

其中：“—”表示汽车在公路圆曲线外侧行驶。

根据公式计算并结合我国的具体情况，《公路工程技术标准》规定了各级公路的圆曲线半径，如表1-2-3所示。

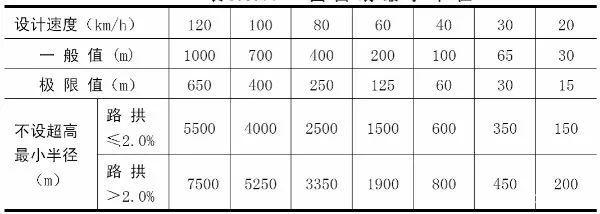
以上三种圆曲线最小半径在具体应用时，应考虑以下几方面的要求：

(1)一般情况下尽量选用大于或等于一般最小半径，只有受地形限制及其他特殊困难时，才可采用极限最小半径；

(2)桥位处两端设置圆曲线时，一般大于一般最小半径；

(3)隧道内必须设置圆曲线时．应大于不设超高的最小半径；

(4)长直线或陡坡尽头，不得采用小半径圆曲线；

(5)不论偏角大小，均应设置圆曲线；

(6)半径过大也无实际意义，故一般宜小于10000m。

例1-2-1 某平原区二级公路，计算行车速度v＝80km/h，试问该公路的极限最小半径为多少?

解：按表1-2-l可知，横向力系数u=0.12，ib=0.08

根据式(1-2-1)极限最小半径为：

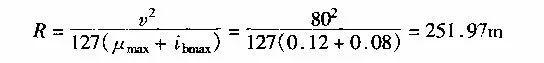
《公路工程技术标淮》规定为250m(表1-2-3)。

例1-2-2某山岭重丘区三级公路，其设计车速v＝30km/h，试问该公路的最小半径为多少?

解：按表(1-2-2)可知，横向力系数u＝0.05，ib=0.06

根据式(1-2-1)一般最小半径为：

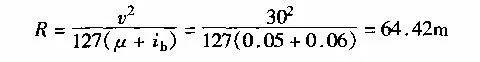
所以，《公路工程技术标准》规定为65m(表1-2-3)。

例1-2-3 已知某平原区高速公路，其计算行车速度v=120km/h，设该公路的路面横坡度i1=1．5％，试计算该公路不设超高的最小半径为多少?

解：已知i1=0.015，设u=0.035

根据式(1-2-5)不设超高的最小半径公式：

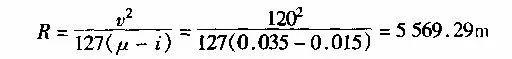
由表1-2-3可知，不设超高最小半径R＝5500m，与《公路工程技术标准》规定相符合。

三、缓和曲线

缓和曲线是设置在直线与圆曲线之间或大圆曲线与小圆曲线之间，由较大圆曲线向较小圆曲线过渡的线形，是道路平面线形要素之一。它的主要特征是曲率均匀变化。《公路工程技术标准》规定，除四级公路可不设缓和曲线外，其他各级公路，当平曲线半径小于不设超高的最小半径时，应设缓和曲线。本节主要讨论缓和曲线的作用、性质、参数、长度和设计方法。

1、缓和曲线的作用与性质

(1)缓和曲线的作用

A．便于驾驶员操纵方向盘

汽车从直线进入圆曲线，或从大半径圆曲线驶入小半径圆曲线时，插入缓和曲线，可使汽车前轮转向角逐渐从0°至a转向，从而有利于驾驶员操纵方向盘．保证安全行驶。

B．满足乘客乘车的舒适与稳定，减小离心力变化

离心力的大小与汽车行驶的曲率半径大小成反比．在直线段中，离心力为零。在圆曲线上，离心力最大。当插人缓和曲线时，因为缓和曲线的曲率是逐渐变化的，可以消除离心力的突变，从而保证乘客乘车舒适与稳定。

C．满足超高、加宽缓和段的过渡，利于平稳行车

当圆曲线上有超高与加宽时，由直线段上无超高及加宽过渡到主圆曲线的全超高及全加宽时，必须有一个缓和段．而设置了缓和曲线．可以通过缓和曲线完成超高及加宽的逐渐过渡。

式(1-2-11)为汽车转弯时的理论轨迹方程，从中可以得出两个结论：—是该曲线上任一点的曲率半径与该点至曲线起点距离成反比，它符合汽车在道路上的行驶轨迹；二是参数A对某一曲线来说，是一个常救，但就整个公路线形而言，其实质为一个放大倍数，它适应于不同的情况，因此，需建立一个数学模型来作为缓和曲线。

2、回旋线基本方程

从回旋线的数学定义可知，其曲率半径ρ随曲线上某一点至该曲线起点之距离成反比(即回旋线为曲率半径ρ随曲线长度增长而减小的曲线)。即

式中：C——曲率与曲线长度的比例常数；

其余符号同前。

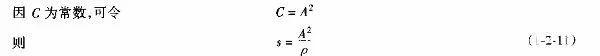
3、缓和曲线最小长度

汽车在缓和曲线上行驶时，要有足够的缓和曲线长度，以保证驾驶员操纵方向盘所需的时间、限制离心加速度的增长率及满足设置超高与加宽过渡等的要求。

（1）根据离心加速度变化率求缓和曲线最小长度

为了保证乘客乘车的舒适性，就需控制离心力的变化率。

as——离心加速度平均增长率，m/s3；

Δa——离心加速度的变化率，m/s3；

t——汽车在缓和曲线上行驶的时间，s，一般取用t=3s。

确定缓和曲线最小长度时，我国公路设计中采用as ≤0.6，则

（2）依驾驶员操纵方向盘所需时间求缓和曲线长度

试验表明，驾驶员在缓和曲线上操纵方向盘的最合适时间为t=3~5s，我国采用t=3s，所以缓和曲线最小长度为

式中：v——计算行车速度，km/h。

上式表明．最短的缓和曲线与半径的大小无关，即使平曲线半径较大，当汽车高速行驶时，也应有个转变过程，因而式(1-2-15)是高等级公路设置缓和曲线的校核式。

（3）根据超高附加纵坡不宜过陡来确定缓和曲线最小长度

超高附加纵坡(即超高渐变率)是指在缓和曲线上设置超高缓和段后，因路基外侧由双向横坡逐渐变成单向超高横坡，所产生的附加纵坡。当附加纵坡过小时，不利于排水；当附加纵坡过大时，路容不美观。

为使缓和曲线有适中的超高渐变率，就需确定其有合适长度。由超高缓和段长度计算公式知

式中：lc——超高缓和段长度，m；

lh——缓和曲线长度，m；

hc——路基外侧全超高断面处的全超高值，m；

ρ——超高渐变李(或称附加纵坡)。

4，从视觉上应有平顺感的要求计算缓和曲线最小长度

式中：lc——超高缓和段长度，m；

lh——缓和曲线长度，m；

hc——路基外侧全超高断面处的全超高值，m；

ρ——超高渐变李(或称附加纵坡)。

4，从视觉上应有平顺感的要求计算缓和曲线最小长度

4、直角坐标及要素计算

(1)回旋线切线角

A．缓和曲线上任意点的切线角βx

缓和曲线的切线角，是指缓和曲线上任一点的切线与该缓和曲线起点的切线所成夹角。如图1-2-4所示，设缓和曲线所在直角坐标系XOY，o为原点．在缓和曲线上任意一点P处取一微分弧段ds，则

(2)缓和曲线直角坐标

在图1-2-4中，任意一点P处取一微分弧段d s，其所对应的中心角为dβx，则

(3)缓和曲线常数

为了能在直线与圆曲线之间插入缓和曲线，必须将原有圆曲线向内移动一定的距离P。圆曲线向内移动有两种方法：—种是圆心不变，使圆曲线半径减小．从而使因曲线向内移动；另一种是半径不变，而圆心沿分角线方向内移，使圆曲线向内移动。由于后者是不平行移动，圆曲线上的各点的内移值不相等，测设工作麻烦，因此采用第一种方法。

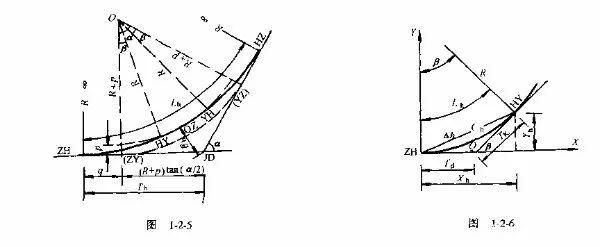
采用圆心不动的平行移动方法，可以看成是平曲线在未设置缓和曲线时的圆曲线半径为R+p，而该平曲线要插入缓和曲线，向内移动距离P后，圆曲线半径正好减小一个P值，即为R，如图1-2-5所示。

A.主曲线的内移值P及切线增长值q

由图1-2-5可知

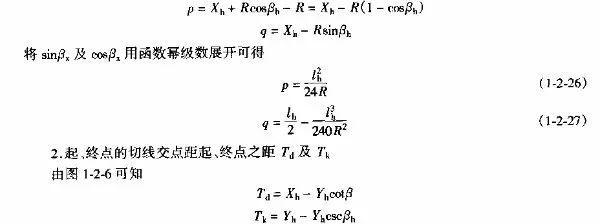
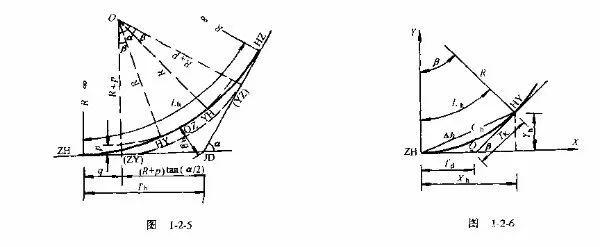
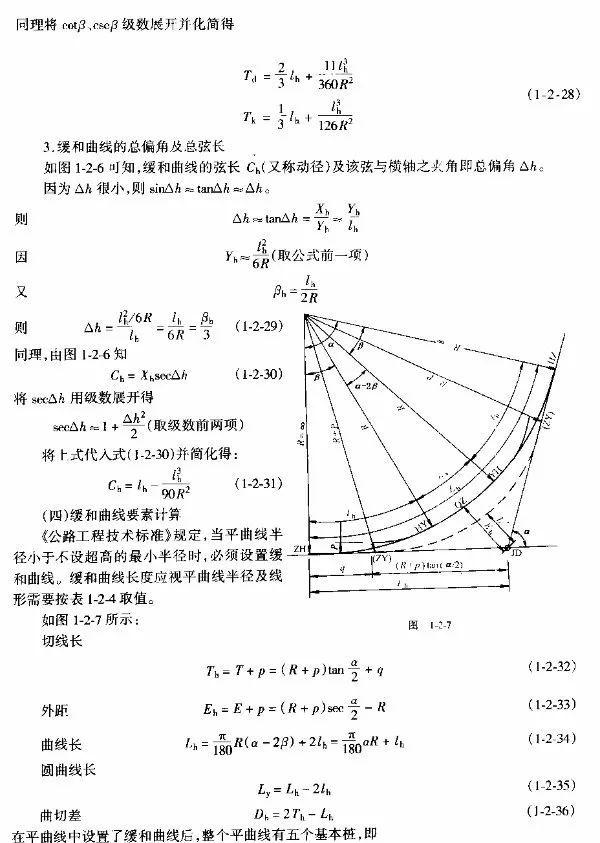
ZH——第一段缓和曲线的起点(直缓点)

HY——第一段缓和曲线的终点(缓圆点)

QZ——平曲线的中点(曲中点)；

YH——第二段缓和曲线的终点(圆缓点)

HZ——第二段缓和曲线的起点(缓直点)；

例1-2-4 某平原微丘区二级公路有一弯道，其平曲线半径及R=260m，交点JD校号

K16+721.26，偏角为a＝29°23′24″，试计算该曲线上设置缓和曲线后的五个基本桩号。

解：

1．确定缓和曲线长度

由题意可知，该公路为平原微丘区二级公路．其设计车速v＝80km／h，则

6．实地敷设步骤：

1)在JD处沿两切线方向分别量取103.37m得平曲线起点(ZH)终点(HZ)的位置；

2)在JD沿分角线方向量取39.30m得平曲线中点(QZ)位置；

3)分别以HZ(或ZH)为坐标原点，沿切线方向分别以Xh和Yh用切线支距法定出YH(或HY)的位置。

更多相关信息 还可关注中铁城际公众号矩阵 扫一扫下方二维码即可关注